Table of contents
Introduction
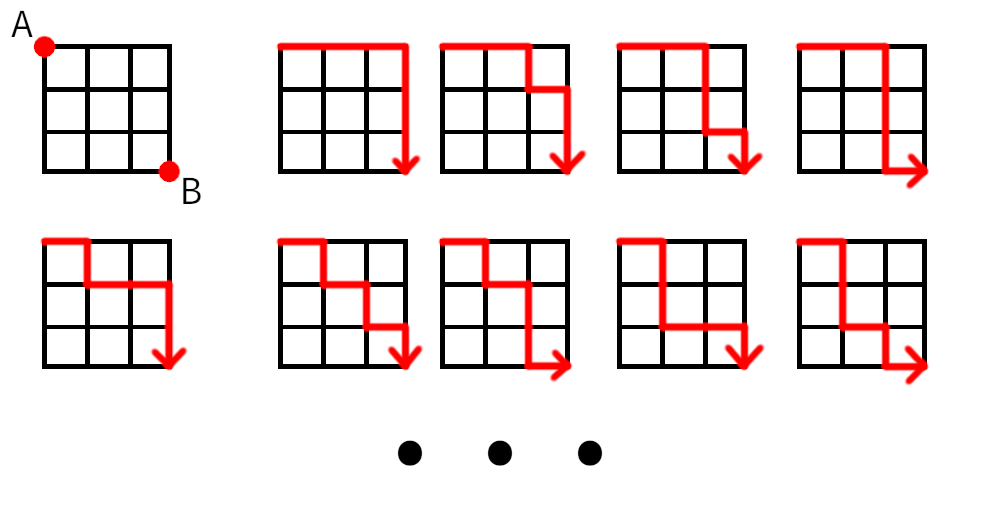
How would you go about determining the number of possible paths in a
grid of size n if your initial position is at the top left corner and
your destination is the bottom right corner, knowing you can only go
right or down at each move? Let’s look at a grid of size 3 × 3:
Even at such a small size, one needs some concentration. Sure, it can be done on paper, but there must be a better way…
Python to the rescue
Once again, programming comes in handy! Life is complicated, but there are aspects of it that can be solved more easily than previously thought when we use the right tools. Knowing that this particular situation corresponds to values from Pascal’s Triangle might help, but it sure is more fun to come up with a different solution. Here is how it occurred to me in Python:
'''
This approach consists in getting the number of possible paths for each
position where we stop in a grid. We know that once we reach the bottom
or the right of the grid, there is only one path possible from there,
so we take advantage of this fact and calculate the total number of
possible paths starting from the bottom right corner. A 2x2 grid would
have 9 indices starting at 0:
012
345
678
We start at index 8 and will calculate the number of possible paths for
all previous positions. From index 8, we calculate that index 4 must
have 2 possible paths to reach index 8 (4>7>8 and 4>5>8). We then find
that index 3 has 3 possible paths since from there we can go right to
index 4 (2 paths) or down to index 6 (1 path). We continue by checking
index 1, which would be the sum of the number of paths at index 4 and
index 2, which is 3 possible paths from there. Now, we are left at the
beginning and the total number of possible paths is index 3 + index 1
(3 + 3 = 6).
The values used would then be tweaked a little depending on the size
of the grid, but the algorithm remains the same. Here is how it works
concretely:
- Get the number of positions in the grid. 2x2 means 9 positions by
counting all intersections. With a 2x2 starting at index 0, we have the
following positions:
012
345
678
- Generate a list corresponding to the length of previously found number
of positions and give a value of 1 to each position. For a 2x2, it is
[1,1,1,1,1,1,1,1,1]
- Determine the multiple to be used to check if an index falls in the
first column (grid_size + 1). The indices in the first column are 0, 3
and 6, so multiple = 3.
- Start from the bottom right corner of the grid (index 8). Get the
index of that position starting at zero (length of positions - 1).
- Start a while loop:
- Check if current position is equal to grid size, meaning we got to
the last position to evaluate. Return the value of the first index if
this is the case.
- Check if current position is a multiple of 3 in that example.
If so, we skip and go back one index. For instance, if index was 6
(multiple of 3), go back to index 5.
- Determine the index of position to the left of current position
and the index of position above current position. Sum the two together
and give that value to the index that corresponds to one step left
and one step up in the grid. Starting at 8, we sum index 7 and index
5 (result = 2) and set that value for index 4, which is the number of
possible paths from that index number.
- Decrement current position by one and repeat the process until we
break out of the loop.
'''
GRID_SIZE = 100
def num_paths(grid_size):
'''Return the number of possible paths in a grid of size `grid_size`
when going only right and down as an integer.'''
num_points = (grid_size + 1) ** 2
path_list = [1] * num_points
multiple = grid_size + 1 # Indices of first column match this multiple
# Last index in list
starting_point = len(path_list) - 1
while True:
if starting_point == grid_size:
return path_list[0]
if starting_point % multiple == 0:
starting_point -= 1
else:
previous = starting_point - 1
previous2 = starting_point - multiple
left_up_index = previous2 - 1
left_up_value = sum([path_list[previous], path_list[previous2]])
path_list[left_up_index] = left_up_value
starting_point -= 1
if __name__ == '__main__':
print(num_paths(GRID_SIZE))
In the end, the idea was to find the number of possible paths that correspond to each possible move, starting from the destination and reverse engineering the number of possibilities until we get to the starting point.
Conclusion
As it turns out, this strategy of reverse engineering things works pretty well when applied to real-life examples. When setting a goal, for instance loosing 10 kilograms in one year, it can sound a lot less daunting to find out what this represents by month (0.83 kg) or even by week (0.19 kg) instead of fixating on the big gap from your current situation. For short-term goals, this can be reduced to daily or even hourly outcomes.
This goes hand in hand with the advice found in Atomic Habits, an excellent book written by James Clear:
A 1% daily improvement leads to a version of yourself that’s 37 times better in one year.
If that’s not motivating enough to start taking little steps with consistency towards your dreams, I don’t know what is.